The introduction of numbers as coordinates is an act of violence - Hermann Weyl
(参照一维连续统的特定划分模式来) 引入一些数作为坐标是一种鲁莽的行为。 - 赫尔曼 外尔
1. 向量
https://github.com/3b1b/manim 向量计算机空间表示
Mathematics requires a small dose, not of genius, but of an imaginative freedom which, in larger dose, would be insanity - Angus K. Rodgers
数学需要的不是天赋, 而是少量的自由想象, 但想象太过自由优惠陷入疯狂。 - 安古斯。罗杰斯
2. 线性组合、张成的空间与基
线行代数紧紧围绕向量的加法与乘法
特点
A. 两个数乘向量的和被称为这两个向量的线性组合
B. 所有可以表示为给定向量线性组合的向量的集合被称为给定向量张成的空间
考虑问题时:单个向量看作箭头(当你只考虑一个向量时),多个向量看作点(当你考虑多个向量时)
Unfortunately, no one can be told what the Matrix is. You have to see ti for yourself. -Morpheus
(Surprisingly apt words on the importance of understanding matrix operations visually)
很遗憾,Matrix是什么是说不清楚的。 你必须得自己亲眼看看。 -墨菲斯
(描述直观理解矩阵操作重要性的绝佳台词) 哈哈哈😄
3. 矩阵与现行变换 (这部分很重要)
Why 使用变换这个词?
答:( 本身 是暗示你用运动的思维去思考,
本质跟函数一样,
输入-》输出(但变化过程很骚操作))
线性变换:
1.lines remain lines(直线依旧是直线),
2.Origin remains fixed (原点保持固定)
答 :网格线保持平行且等距分布(Grid lines remain parallel and evenly spaced)
**公式: **
V(vector) = x (^i) + y (^j)
Transformed V (verctor) = x (Transformed ^i) + y (Transformed ^j)
Now 引出矩阵 2*2矩阵 :

It is my experience that proofs involving matrices can be shortened by 50% if one throws the matrices out. -Emil Artin
据我的经验,如果丢掉矩阵的话, 那些涉及矩阵的证明可以缩短一半。 -诶米尔 阿廷
4. 矩阵乘法与线性复合
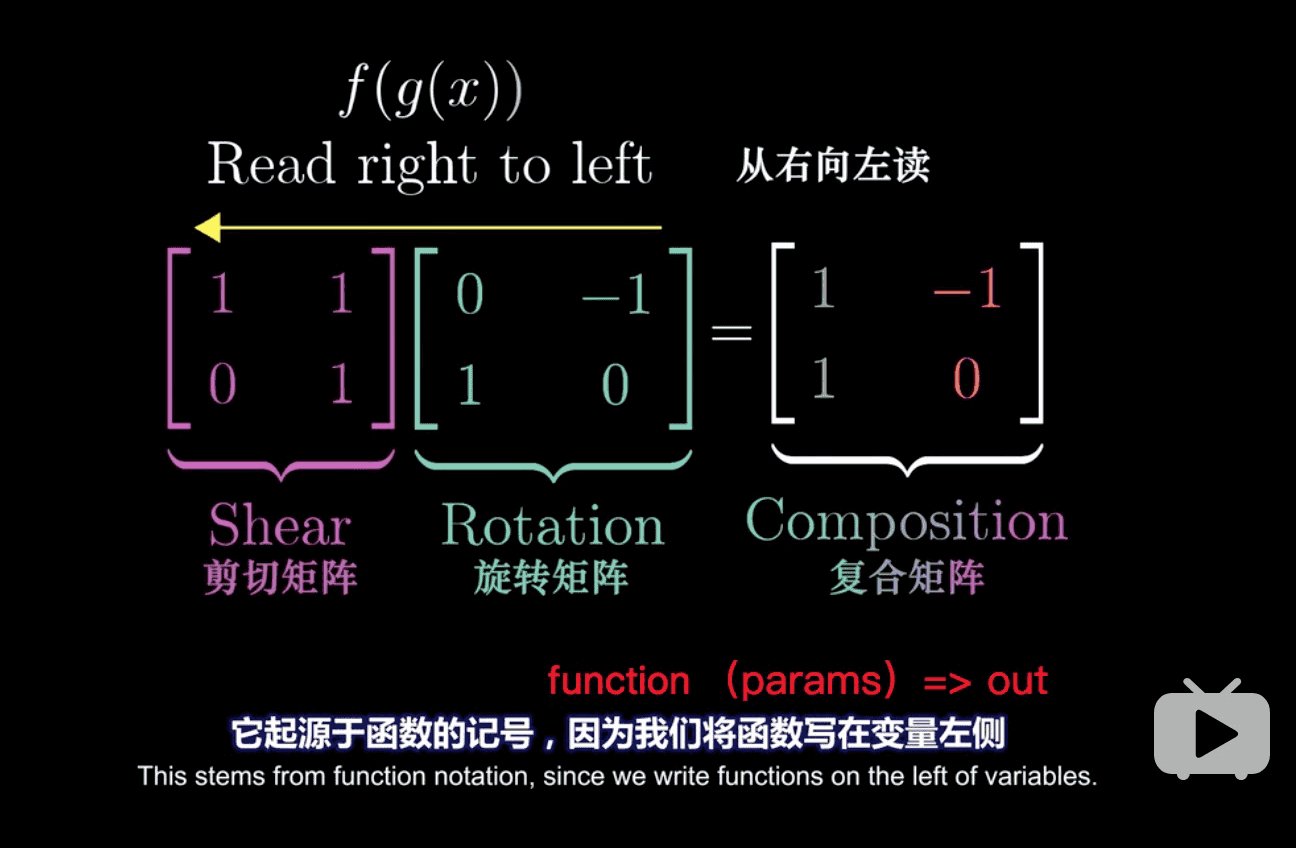
计算过程:

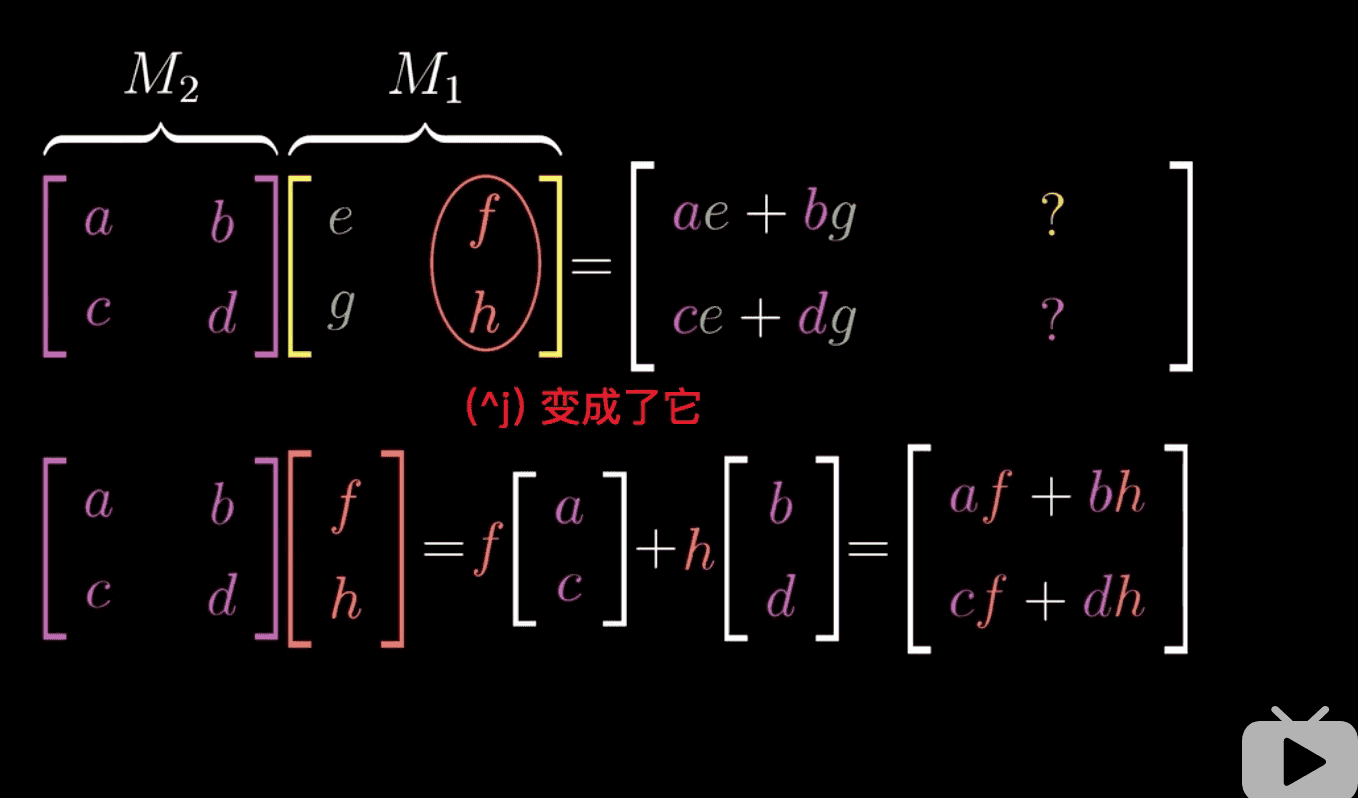
大学记得那公式早就忘了,so 拼命记公式有TM啥子意义浪费时间

Lisa: Well, where’s my dad?
Frink: Well, it should be obvious to even the most
dimwitted individual who holds an advanced degree
in hyperbolic topology that Homer Simpson has stumbled
Into … (dramatic pause) … the third dimension
Lisa: 呃,我爸爸到底在哪里?
Frink: 对于能拿到双曲拓扑学高等学位的傻瓜来说,
这一点也足够显示—-Homer Simpson 误入了 …(关灯)… 三维空间
—-(辛普森一家 第七季第六集)
6. 三维空间中的线性变换(理论同二维空间的一样)
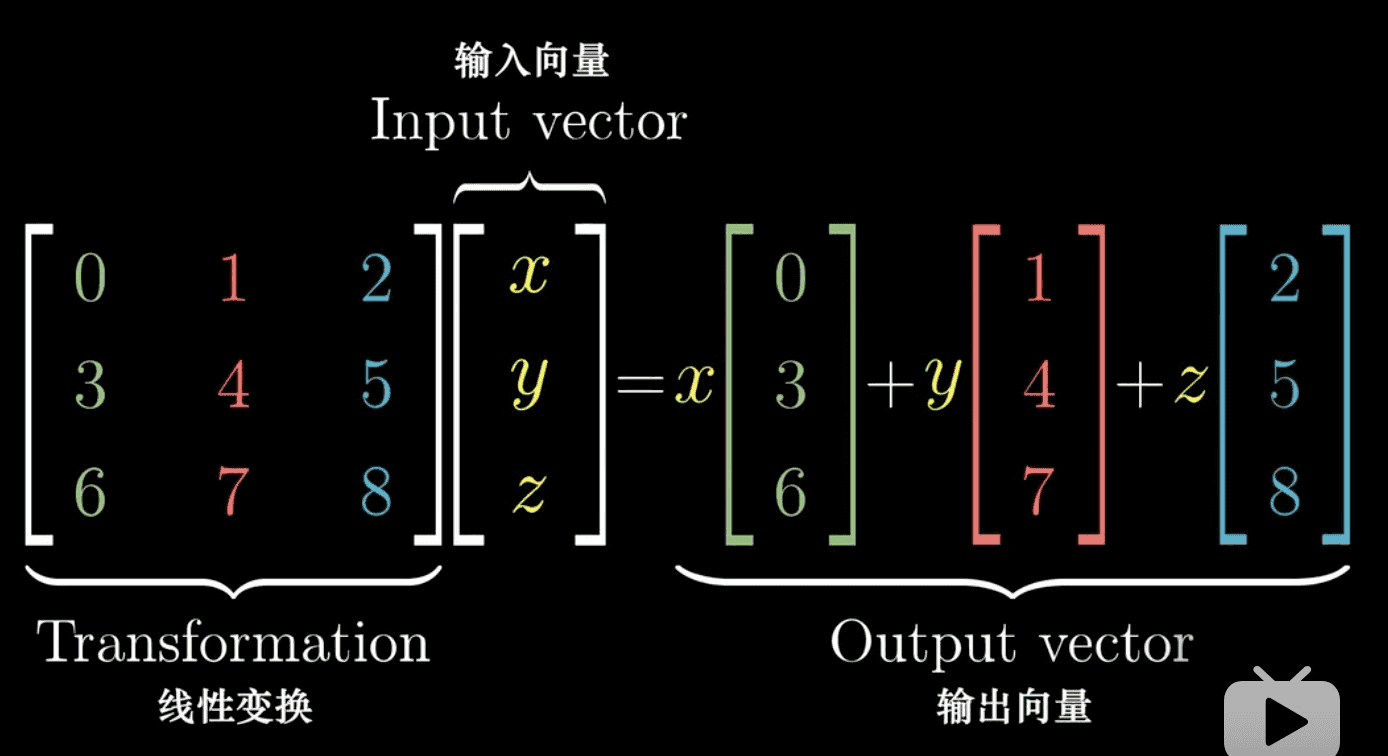
复合变换
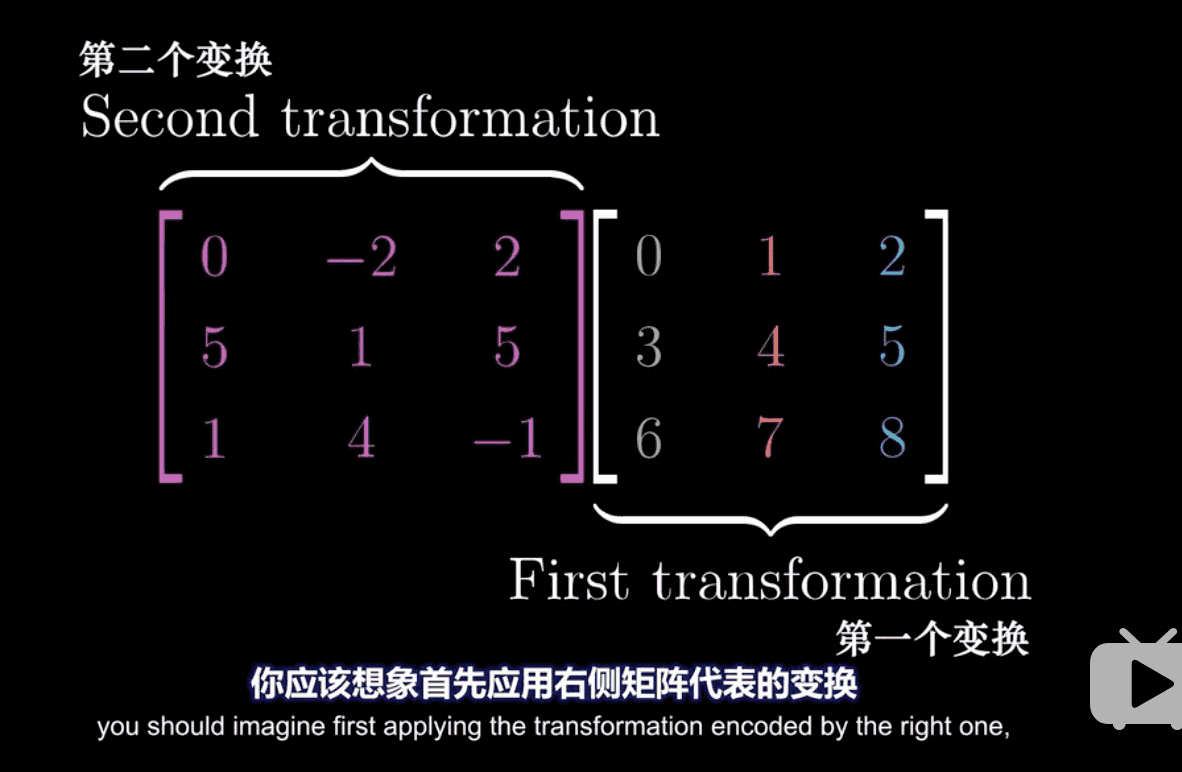
The purpose of computation is insight, not numbers. -Richard Hamming
计算的目的不在于数字本身,而在于洞察其背后的意义。-理查德 哈明
7. 行列式
对空间有多少拉伸和挤压(就是测量一个给定区域面积增大或减小的比例)
例子:
((1,0)(0,1)==》(3,0)(0,2))面积增大了6倍

((1,0)(0,1)==》(1,0)(1,2))面积增大了1倍

总结(这种特殊的缩放比例下(线性状态下改变面积的比例)=》线性变换的行列式 )
公式

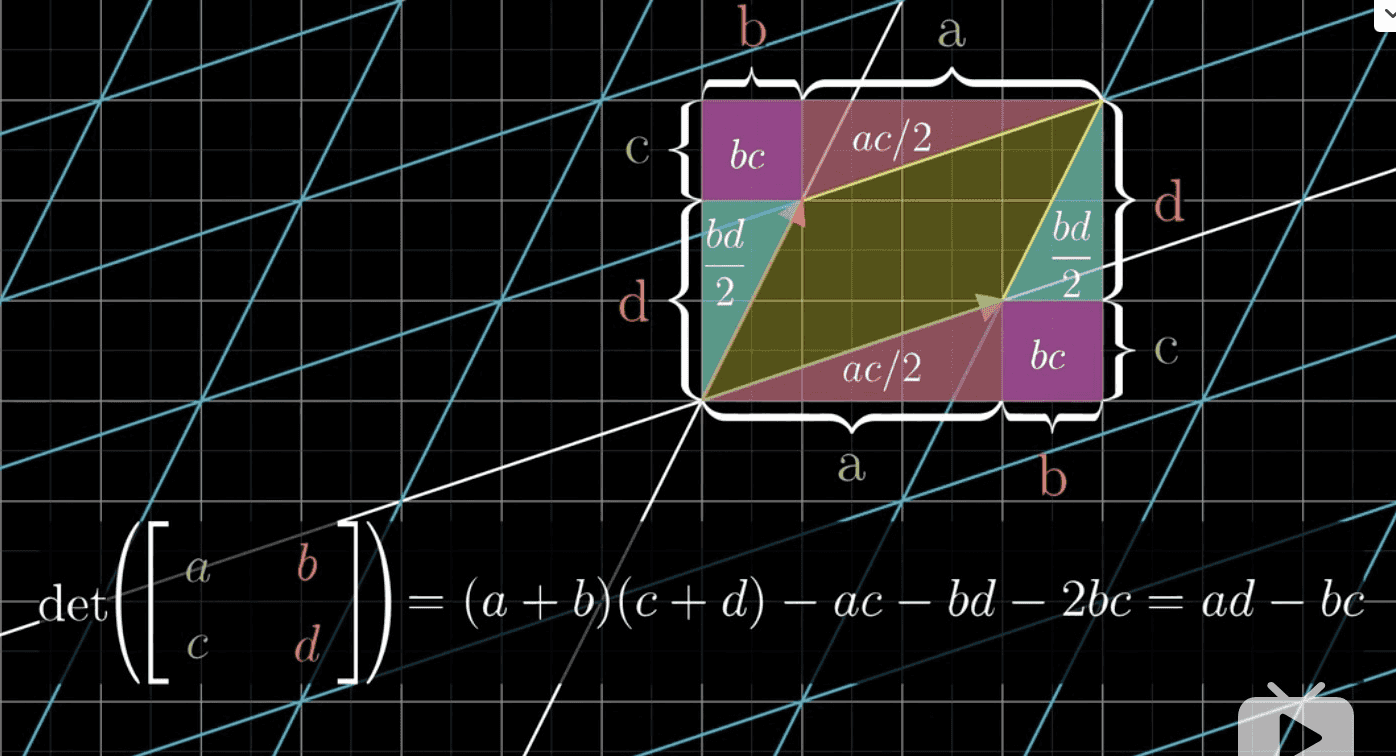

To ask the right question is harder than to answer it - Georg Cantor
提出正确的问题比回答它更困难。 -格奥尔格 康托尔
8. 逆矩阵、列空间与零空间
逆矩阵: 反向寻找源矩阵
秩: 变换后空间的维度
列空间: (不管一条直线,一个平面还是三维空间等,所有可能变换结果的空间的集合)
零空间或核 (变换后落在原点的向量的集合)
On this quiz, I asked you to find the determinant of a 2*3 matrix. Some of you,
To my great amusement, actually tried to do this. -(Via mathprofessorquotes.com, no name listed)
在这个小测试里, 我让你们球一个2*3的矩阵的行列式。让我感到非常可笑的是,你们当中竟然有人尝试去做。 - 摘自mathprofessorquotes.com, 作者秩名
Calvin: You know, I don’t think math is a science, I think it’s a religion.
Hobbes: A religion?
Calvin: Yeah, All these equations are like miracles. You take two numbers and when you add them. They magically become one NEW
Number! No one can say how it happens. You either believe it or you don’t.
卡尔文: 你知道吗,我觉得数学不是一门科学,而是一种宗教。
雷布斯:一种宗教?
卡尔文: 是啊。 这些公式就像奇迹一半。你取出两个数,把他们相加时,
它们神奇地成为了一个全新的数!没人能说清这些到底是什么发生的。你要么完全相信,要么完全不信。
10.点积与对偶性
